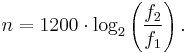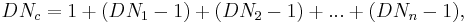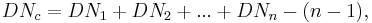Interval (music)

In music theory, an interval is a combination of two notes, or the distance between their pitches. Two-note combinations are also called dyads. Although chords are often defined as sets of three or more notes, intervals are sometimes considered to be the simplest kind of chord.^[1]

Intervals may be described as:^[2]

Vertical or harmonic, if the two notes sound simultaneously
Horizontal, linear, or melodic if they sound successively.

Intervals may be roughly classified as:

Diatonic intervals, between the notes of a diatonic scale,
Chromatic intervals, non-diatonic intervals between the notes of a chromatic scale,
Minute intervals (commas, and microtones), sometimes so small that the difference in pitch between the two notes cannot be perceived.

Interval width

The size or width of an interval can be represented using two alternative and equivalently valid methods, each appropriate to a different context: frequency ratios or cents.

Frequency ratios

The size of an interval between two pitches may be measured by the ratio of their frequencies. Important intervals are those measured by fractions of small numbers, such as 1:1 (unison or prime), 2:1 (octave), 3:2 (perfect fifth), 4:3 (perfect fourth), etc. (see: Limit in music). This system is frequently used to describe intervals in both Western and non-Western music. This method is also often used in just intonation, and in theoretical explanations of equal-tempered intervals used in European tonal music, to explain them through their approximation of just intervals.

Cents

The standard system for comparing interval sizes is with cents. This is a logarithmic scale in which the octave is divided into 1200 equal parts. In equal temperament, each semitone is exactly 100 cents.

The size in cents of the interval from frequency f₁ to frequency f₂ is

$n = 1200 \cdot \log_2 \left( \frac{f_2}{f_1} \right).$

Main intervals

The table shows the most widely used conventional names for the intervals between the notes of a chromatic scale. A semitone is any interval between two adjacent notes in a chromatic scale, a whole tone is any interval spanning two semitones, and a tritone is any interval spanning three tones, or six semitones. In Latin nomenclature, the term ditonus was originally used to indicate any interval composed of two tones, but in current English the corresponding term ditone is used with a much more specific meaning, to refer only to a major third with frequency ratio 81:64.

Intervals with different names but spanning the same number of semitones may have the same width, provided that the instrument is tuned so that the 12 notes of the chromatic scale are equally spaced (a commonly used tuning system called equal temperament). However, they are defined by different notes. For instance, the interval from D to F♯ is a major third, while that from D to G♭ is a diminished fourth, although they have identical width in equal temperament (4 semitones, or 400 cents).

Except for the Latin ones, the names listed here cannot be determined by counting semitones alone. The rules to determine them are explained below. Other names, determined with different naming conventions, are listed in a separate section.

Number of semitones	Diatonic interval	Short	Chromatic interval	Short	Latin nomenclature	Short	Audio
0	Perfect Unison	P1	Diminished second	d2			Play
1	Minor second	m2	Augmented unison	A1	Semitone	S	Play
2	Major second	M2	Diminished third	d3	Whole tone	T	Play
3	Minor third	m3	Augmented second	A2			Play
4	Major third	M3	Diminished fourth	d4			Play
5	Perfect fourth	P4	Augmented third	A3			Play
6	Diminished fifth			d5	Tritone	TT	Play
6	Augmented fourth			A4	Tritone	TT	Play
7	Perfect fifth	P5	Diminished sixth	d6			Play
8	Minor sixth	m6	Augmented fifth	A5			Play
9	Major sixth	M6	Diminished seventh	d7			Play
10	Minor seventh	m7	Augmented sixth	A6			Play
11	Major seventh	M7	Diminished octave	d8			Play
12	Perfect octave	P8	Augmented seventh	A7			Play

Interval number and quality

Interval names (assuming treble clef)

In Western music theory, to name an interval we typically need to determine its number (also called diatonic number) and quality. For instance, major third (or M3) is an interval name, in which the term major (M) describes the quality of the interval, and third (3) indicates its number.

Number

Staff, with staff positions indicated.

As shown above, intervals are labeled according to the number of staff positions they encompass, counting both the lines and gaps between lines, starting with one at the lower note. The number of staff positions from C to G for example is 5, therefore the interval C-G is a fifth (denoted P5 in the figure above).

In a diatonic scale, the number of staff positions conicides with the number of scale steps. This is not true for other kinds of scales, such as the chromatic scale. However, if you take away any accidentals from the notes which form an interval, by definition the notes do not change their staff position. As a consequence, the interval number for any chromatic interval is the same as the interval number of the diatonic interval formed by the two notes without accidentals. This is the reason why interval numbers are also called diatonic interval numbers, and this convention is called diatonic interval numbering.

The rule to determine the diatonic number of a compound interval (an interval larger than one octave), based on the diatonic numbers of the simple intervals from which it is built is explained in a separate section.

Quality

The name of any interval is further qualified using the terms perfect (P), major (M), minor (m), augmented (A), and diminished (d). This is called its interval quality. It is possible to have doubly-diminished and doubly-augmented intervals, but these are quite rare, as they occur only in chromatic contexts. The quality of a compound interval is the quality of the simple interval on which it is based (see here for details).

Major/minor
Major and minor intervals are so-called because certain diatonic intervals (seconds, thirds, sixths, sevenths, and their compounds) may occur in two sizes in the diatonic scale. The larger of the two versions is called major, the smaller one minor. For example, the third occurs both as three semitones away from Re, Mi, La, and Ti in the major scale (or in the C major diatonic scale, three semitones above D, E, A, and B), and four semitones away from Do, Fa, and Sol, (or C, F, and G). The smaller, three-semitone version is called the "minor third" and the larger, four-semitone one is called the "major third". Major intervals invert to minor ones, and vice-versa. For example, a major second inverts to a minor seventh, and the reverse.

Perfect
Perfect intervals are so-called because of their high levels of consonance, and because the inversion of a perfect interval is also perfect. Other kinds of intervals have an opposite quality with respect to their inversion. The inversion of a major interval is a minor interval, the inversion of an augmented interval is a diminished interval. Within the diatonic scale all fourths and fifths are perfect, with five and seven semitones respectively, except for one occurrence each of six semitones: the fourth between Fa and Ti (an augmented fourth), and its inversion, i.e. the fifth between Ti and Fa (a diminished fifth).

Augmented/diminished
Augmented and diminished intervals are so called because they exceed or fall short of either a perfect interval, or a major/minor pair by one semitone, while having the same interval number (i.e. encompassing the same number of staff positions). Except for the augmented fourth (Fa-Ti) and diminished fifth (Ti-Fa), they do not appear in the diatonic scale. For instance, there is no three-semitone interval in the diatonic scale that functions as a second, and the augmented second (e.g., E♭–F♯) is three semitones wide.

Example

Neither the number, nor the quality of an interval can be determined by counting semitones alone. As explained above, the number of staff positions must be taken into account as well.

For example, as shown in the table below, there are four semitones between A and C♯, between A and D♭, between A♯ and D, and between A♭ and B♯, but

the interval A-C♯ is called a major third (as it spans 3 staff positions),
the intervals A-D♭ and A♯-D are called diminished fourths (as they span 4 staff positions),
the interval A♭-B♯ is called a doubly augmented second (as it spans 2 staff positions).

Number of semitones	Interval name	Staff positions
Number of semitones	Interval name	1	2	3	4
4	major third	A		C♯
4	diminished fourth	A			D♭
4	diminished fourth	A♯			D
4	doubly augmented second	A♭	B♯

The diminished fourth is an interval found between the seventh and third degrees of the harmonic minor scale, while the doubly augmented second only occurs in entirely chromatic contexts. In equal-tempered tuning, as on a piano, these intervals are indistinguishable by sound when played in isolation, but in musical context the diatonic function of the notes incorporated is very different.

Shorthand notation

Intervals are often abbreviated with a P for perfect, m for minor, M for major, d for diminished, A for augmented, followed by the interval number. The indication M and P are often omitted. The octave is P8, and a unison is usually referred to simply as "a unison" but can be labeled P1. The tritone, an augmented fourth or diminished fifth is often TT. The interval qualities may be also abbreviated with perf, min, maj, dim, aug. Examples:

m2 (or min2): minor second,
M3 (or maj3): major third,
A4 (or aug4): augmented fourth,
d5 (or dim5): diminished fifth,
P5 (or perf5): perfect fifth.

Intervals in chords

Main articles: Chord (music) and Chord symbol

Chords are sets of three or more notes. They are typically defined as the combination of intervals starting from a common note called the root of the chord. For instance a major triad is a chord containing three notes defined by the root and two intervals (major third and major fifth). Sometimes even a single interval (dyad) is considered to be a chord.^[1] Chords are classified based on the quality and number of the intevals which define them. The main chord qualities are minor, major, diminished, augmented, half-diminished, and dominant.

The symbols used for chord quality are similar to those used for interval quality (see above). In addition, + or aug is used for augmented, ° or dim for diminished, ^ø for half diminished, and dom for dominant (the symbol − is not used for diminished, as it is sometimes questionably used for minor). Furthermore, without contrary information a major third and a perfect fifth are implied. Maj and min, or M and m, always at least (but not only) refer to the third interval, while aug and dim, or + and °, always at least (but not only) refer to the fifth. The 3 for the third, and the 5 for the fifth are typically omitted. A plain 7 (or dom7) stands for a 4-note chord formed by a minor seventh interval, together with the implied M.

The table shows the intervals contained in some of the main chords (component intervals), and some of the symbols used to denote them. The interval qualities or numbers in boldface font are those conventionally used to name the chord or build its symbol.

Main chords		Component intervals
Name	Symbol (C is used as root)	Third	Fifth	Seventh
Major triad	C	maj3	perf5
Major triad	CM, or Cmaj (rarely CM3, or Cmaj3)	maj3	perf5
Minor triad	Cm, or Cmin (rarely Cm3, or Cmin3)	min3	perf5
Augmented triad	C+, or Caug (rarely C+5, or Caug5)	maj3	aug5
Diminished triad	C°, or Cdim (rarely C°5, or Cdim5)	min3	dim5
Dominant seventh chord	C7, or Cdom7	maj3	perf5	min7
Minor seventh chord	Cm7, or Cmin7	min3	perf5	min7
Major seventh chord	CM7, or Cmaj7	maj3	perf5	maj7
Diminished seventh chord	C°7, or Cdim7	min3	dim5	dim7
Half-diminished seventh chord	C^ø7	min3	dim5	min7

Classification

The intervals contained in the table are diatonic to C major. All other intervals are chromatic to C major.

Intervals can be described, classified, or compared with each other according to various criteria.

Melodic and harmonic

Main articles: Harmony and Melody

An interval can be described as

Vertical or harmonic if the two notes sound simultaneously
Horizontal, linear, or melodic if they sound successively.^[3]

Diatonic and chromatic

A diatonic interval is an interval formed by two notes of a diatonic scale. The table on the right depicts all diatonic intervals for C major.

Consonant and dissonant

Consonance and dissonance are relative terms that refer to the stability, or state of repose, of particular musical effects. Dissonant intervals are those that cause tension, and desire to be resolved to consonant intervals.

These terms are relative to the usage of different compositional styles.

In the Middle Ages, only the unison, octave, perfect fourth, and perfect fifth were considered consonant harmonically.
In 16th-century usage, perfect fifths and octaves, and major and minor thirds and sixths were considered harmonically consonant, and all other intervals dissonant. In the common practice period, it makes more sense to speak of consonant and dissonant chords, and certain intervals previously thought to be dissonant (such as minor sevenths) became acceptable in certain contexts. However, 16th-century practice continued to be taught to beginning musicians throughout this period.
Hermann von Helmholtz (1821–1894) defined a harmonically consonant interval as one in which the two pitches have an overtone in common (specifically excluding the seventh harmonic). This essentially defines all seconds and sevenths as dissonant, while perfect fourths and fifths, and major and minor thirds and sixths, are consonant.
Pythagoras defined a hierarchy of consonance based on how small the numbers are that express the ratio. 20th-century composer and theorist Paul Hindemith's system has a hierarchy with the same results as Pythagoras's, but defined by fiat rather than by interval ratios, to better accommodate equal temperament, all of whose intervals (except the octave) would be dissonant using acoustical methods.
David Cope (1997) suggests the concept of interval strength^[4], in which an interval's strength, consonance, or stability is determined by its approximation to a lower and stronger, or higher and weaker, position in the harmonic series. See also: Lipps-Meyer law.

All of the above analyses refer to vertical (simultaneous) intervals.

Simple and compound

A simple interval is an interval spanning at most one octave. Intervals spanning more than one octave are called compound intervals.^[5]

In general, a compound interval may be defined by a sequence or "stack" of two or more simple intervals of any kind. For instance, a major tenth (two staff positions above one octave), also called compound major third, spans one octave plus one major third. A major seventeenth (two staff positions above two octaves) is another example of compound major third, and can be built either by adding up two octaves and one major third, or four perfect fifths.

Any compound interval can be always decomposed into one or more octaves plus one simple interval. For instance, a seventeenth can be always decomposed into two octaves and one major third, and this is the reason why it is called a compound major third, even when it is built using four fifths.

The diatonic number DN_c of a compound interval formed from n simple intervals with diatonic numbers DN₁, DN₂, ..., DN_n, is determined by:

$DN_c = 1 + (DN_1 - 1) + (DN_2 - 1) + ... + (DN_n - 1), \$

which can also be written as:

$DN_c = DN_1 + DN_2 + ... + DN_n - (n - 1), \$

The quality of a compound interval is determined by the quality of the simple interval on which it is based. For instance, a compound major third is a major tenth (1+(8-1)+(3-1) = 10), or a major seventeenth (1+(8-1)+(8-1)+(3-1) = 17), and a compound perfect fifth is a perfect twelfth (1+(8-1)+(5-1) = 12) or a perfect nineteenth (1+(8-1)+(8-1)+(5-1) = 19). Notice that two octaves are a fifteenth, not a sixteenth (1+(8-1)+(8-1) = 15). Similarly, three octaves are a twentysecond (1+3*(8-1) = 22), and so on.

Intervals larger than a seventeenth seldom need to be spoken of, most often being referred to by their compound names, for example "two octaves plus a fifth"^[6] rather than "a 19th".

Steps and skips

Linear (melodic) intervals may be described as steps or skips in a diatonic context. Steps are linear intervals between consecutive scale degrees while skips are not, although if one of the notes is chromatically altered so that the resulting interval is three semitones or more (e.g. C to D♯), that may also be considered a skip. However, the reverse is not true: a diminished third, an interval comprising two semitones, is still considered a skip.

The words conjunct and disjunct refer to melodies composed of steps and skips, respectively.

Enharmonic intervals

Two intervals are considered to be enharmonic, or enharmonically equivalent, if they both contain the same pitches spelled in different ways; that is, if the notes in the two intervals are themselves enharmonically equivalent. Enharmonic intervals span the same number of semitones. For example, as shown in the matrix below, F♯–A♯ (a major third), G♭–B♭ (also a major third), F♯–B♭ (a diminished fourth), and G♭–A♯ (a doubly augmented second) are all enharmonically equivalent. In fact, although they have a different name and staff position, F♯ and G♭ indicate the same pitch, and the same is true for A♯ and B♭. As a consequence, all these intervals span four semitones.

Number of semitones	Interval name	Staff positions
Number of semitones	Interval name	1	2	3	4
4	major third	F♯		A♯
4	major third		G♭		B♭
4	diminished fourth	F♯			B♭
4	doubly augmented second		G♭	A♯

Size of intervals used in different tuning systems

Number of semitones	Name	5-limit tuning (pitch ratio)	Comparison of interval width (in cents)
Number of semitones	Name	5-limit tuning (pitch ratio)	5-limit tuning	Pythagorean tuning	1/4-comma meantone	Equal temperament
0	Perfect unison	1:1	0	0	0	0
1	Minor second	16:15	112	90	117	100
2	Major second	9:8	204	204	193	200
3	Minor third	6:5 75:64 32:27	316 (wolf) 275 294	294 318	310 (wolf) 269	300
4	Major third	5:4 512:405 32:25 81:64	386 406 (wolf) 427 408	408 384	386 (wolf) 427	400
5	Perfect fourth	4:3 675:512 27:20	498 478 520	498 (wolf) 522	503 (wolf) 462	500
6	Augmented fourth Diminished fifth	45:32 64:45	590 610	612 588	579 621	600
7	Perfect fifth	3:2 40:27 1024:675	702 680 722	702 (wolf) 678	697 (wolf) 738	700
8	Minor sixth	8:5	814	792	814	800
9	Major sixth	5:3	884	906	890	900
10	Minor seventh	9:5 16:9	1018 996	996	1007	1000
11	Major seventh	15:8	1088	1110	1083	1100
12	Perfect octave	2:1	1200	1200	1200	1200

In this table, the interval widths used in four different tuning systems are compared. To facilitate comparison, just intervals as provided by 5-limit tuning (see symmetric scale n.1) are shown in bold font, and the values in cents are rounded to integers. Notice that in each of the non-equal tuning systems, by definition the width of each type of interval (including the semitone) changes depending on the note from which the interval starts. This is the price paid for seeking just intonation. However, for the sake of simplicity, for some types of interval the table shows only one value (the most often observed one).

In 1/4-comma meantone, by definition 11 perfect fifths have a size of approximately 697 cents (700−ε cents, where ε ≈ 3.42 cents); since the average size of the 12 fifths must equal exactly 700 cents (as in equal temperament), the other one must have a size of about 700+11ε cents, which is about 738 cents (the wolf fifth); 8 major thirds have size about 386 cents (400−4ε), 4 have size about 427 cents (400+8ε), and their average size is 400 cents. In short, similar differences in width are observed for all interval types, except for unisons and octaves, and they are all multiples of ε (the difference between the 1/4-comma meantone fifth and the average fifth). A more detailed analysis is provided here. Note that 1/4-comma meantone was designed to produce just major thirds, but only 8 of them are just (5:4, about 386 cents).

The Pythagorean tuning is characterized by smaller differences because they are multiples of a smaller ε (ε ≈ 1.96 cents, the difference between the Pythagorean fifth and the average fifth). Notice that here the fifth is wider than 700 cents, while in most meantone temperaments, including 1/4-comma meantone, it is tempered to a size smaller than 700. A more detailed analysis is provided here.

The 5-limit tuning system uses just tones and semitones as building blocks, rather than a stack of perfect fifths, and this leads to even more varied intervals throughout the scale (each kind of interval has three or four different sizes). A more detailed analysis is provided here. Note that 5-limit tuning was designed to maximize the number of just intervals, but even in this system some intervals are not just (e.g., 3 fifths, 5 major thirds and 6 minor thirds are not just; also, 3 major and 3 minor thirds are wolf intervals).

The above mentioned symmetric scale 1, defined in the 5-limit tuning system, is not the only method to obtain just intonation. It is possible to construct juster intervals or just intervals closer to the equal-tempered equivalents, but most of the ones listed above have been used historically in equivalent contexts. In particular, the asymmetric version of the 5-limit tuning scale provides a juster value for the minor seventh (9:5, rather than 16:9). Moreover, the tritone (augmented fourth or diminished fifth), could have other just ratios; for instance, 7:5 (about 583 cents) or 17:12 (about 603 cents) are possible alternatives for the augmented fourth (the latter is fairly common, as it is closer to the equal-tempered value of 600 cents). The 7:4 interval (about 969 cents), also known as the harmonic seventh, has been a contentious issue throughout the history of music theory; it is 31 cents flatter than an equal-tempered minor seventh. Some assert the 7:4 is one of the blue notes used in jazz. For further details about reference ratios, see here.

In the diatonic system, every interval has one or more enharmonic equivalents, such as augmented second for minor third.

Minute intervals

Main articles: Comma and Microtone

There are also a number of minute intervals not found in the chromatic scale or labeled with a diatonic function, which have names of their own. They may be described as microtones. Except for the quarter tone, the equivalents in cents are approximate, and they can be also classified as commas, as they describe small discrepancies, observed in some tuning systems, between enharmonically equivalent notes.

A Pythagorean comma is the difference between twelve justly tuned perfect fifths and seven octaves. It is expressed by the frequency ratio 531441:524288 (23.5 cents).
A syntonic comma is the difference between four justly tuned perfect fifths and two octaves plus a major third. It is expressed by the ratio 81:80 (21.5 cents).
A septimal comma is 64:63 (27.3 cents), and is the difference between the Pythagorean or 3-limit "7th" and the "harmonic 7th".
A diesis is generally used to mean the difference between three justly tuned major thirds and one octave. It is expressed by the ratio 128:125 (41.1 cents). However, it has been used to mean other small intervals: see diesis for details.
A diaschisma is the difference between three octaves and four justly tuned perfect fifths plus two justly tuned major thirds. It is expressed by the ratio 2048:2025 (19.6 cents).
A schisma (also skhisma) is the difference between five octaves and eight justly tuned fifths plus one justly tuned major third. It is expressed by the ratio 32805:32768 (2.0 cents). It is also the difference between the Pythagorean and syntonic commas. (A schismic major third is a schisma different from a just major third, eight fifths down and five octaves up, F♭ in C.)
A kleisma is the difference between six minor thirds and one tritave or perfect twelfth (an octave plus a perfect fifth), with a frequency ratio of 15625:15552 (8.1 cents) (Play).
A septimal kleisma is six major thirds up, five fifths down and one octave up, with ratio 225:224 (7.7 cents).
A quarter tone is half the width of a semitone, which is half the width of a whole tone. It is equal to exactly 50 cents.

See Musical interval mnemonics at Wikibooks for popular musical fragments that feature common intervals

Inversion

Interval inversions

Major 13th (compound Major 6th) inverts to a minor 3rd by moving the bottom note up two octaves, the top note down two octaves, or both notes one octave

A simple interval (i.e., an interval shorter than or equal to an octave) may be inverted by raising the lower pitch an octave, or lowering the upper pitch an octave. For example, the fourth from a lower C to a higher F may be inverted to make a fifth, from a lower F to a higher C.

There are two rules to determine the number and quality of the inversion of any simple interval:^[7]

The interval number and the number of its inversion always add up to nine (4 + 5 = 9, in the example just given).
The inversion of a major interval is a minor interval, and vice versa; the inversion of a perfect interval is also perfect; the inversion of an augmented interval is a diminished interval, and vice versa; the inversion of a doubly augmented interval is a doubly diminished interval, and vice versa.

For example, the interval from C to the E♭ above it is a minor third. By the two rules just given, the interval from E♭ to the C above it must be a major sixth.

Since compound intervals are larger than an octave, "the inversion of any compound interval is always the same as the inversion of the simple interval from which it is compounded."^[8]

For intervals identified by their ratio, the inversion is determined by reversing the ratio and multiplying by 2. For example, the inversion of a 5:4 ratio is an 8:5 ratio.

For intervals identified by an integer number of semitones, the inversion is obtained by subtracting that number from 12.

Since an interval class is the lower number selected among the interval integer and its inversion, interval classes cannot be inverted.

Interval root

Although intervals are usually designated in relation to their lower note, David Cope^[4] and Hindemith^[9] both suggest the concept of interval root. To determine an interval's root, one locates its nearest approximation in the harmonic series. The root of a perfect fourth, then, is its top note because it is an octave of the fundamental in the hypothetical harmonic series. The bottom note of every odd diatonically numbered intervals are the roots, as are the tops of all even numbered intervals. The root of a collection of intervals or a chord is thus determined by the interval root of its strongest interval.

As to its usefulness, Cope^[4] provides the example of the final tonic chord of some popular music being traditionally analyzable as a "submediant six-five chord" (added sixth chords by popular terminology), or a first inversion seventh chord (possibly the dominant of the mediant V/iii). According the interval root of the strongest interval of the chord (in first inversion, CEGA), the perfect fifth (C–G), is the bottom C, the tonic.

Interval cycles

Interval cycles, "unfold [i.e. repeat] a single recurrent interval in a series that closes with a return to the initial pitch class", and are notated by George Perle using the letter "C", for cycle, with an interval-class integer to distinguish the interval. Thus the diminished-seventh chord would be C3 and the augmented triad would be C4. A superscript may be added to distinguish between transpositions, using 0–11 to indicate the lowest pitch class in the cycle.^[10]

Alternative interval naming conventions

As shown below, some of the above mentioned intervals have alternative names, and some of them take a specific alternative name in Pythagorean tuning, five-limit tuning, or meantone temperament tuning systems such as quarter-comma meantone. Notice that ditone and semiditone are specific for Pythagorean tuning, while tone and tritone are used generically for all tuning systems. Interestingly, despite its name, a semiditone (3 semitones, or about 300 cents) can hardly be viewed as half of a ditone (4 semitones, or about 400 cents). All the intervals with prefix sesqui- are justly tuned, and their frequency ratio, shown in the table, is a superparticular number (or epimoric ratio). The same is true for the octave.

The diminished second is a comma, but some commas are not diminished seconds. For intance, the Pythagorean comma (531441:524288) is the opposite of a diminished second. 5-limit tuning defines four kinds of comma, three of which meet the definition of diminished second, and hence are listed in the table below. The fourth one, called syntonic comma (81:80) can neither be regarded as a diminished second, nor as its opposite. See here for further details.

Number of semitones	Generic names				Specfic names
	Quality and number		Other naming conventions		Pythagorean tuning	5-limit tuning	1/4-comma meantone
	Full	Short	Other naming conventions		Pythagorean tuning	5-limit tuning	1/4-comma meantone
0	diminished second	d2			descending Pythagorean comma (524288:531441)	lesser diesis (128:125)
0	diminished second	d2			descending Pythagorean comma (524288:531441)	diaschisma (2048:2025) greater diesis (648:625)
1	minor second	m2	semitone, half tone, half step	diatonic semitone, minor semitone	limma (256:243)
1	augmented unison	A1	semitone, half tone, half step	chromatic semitone, major semitone	apotome (2187:2048)
2	diminished third	d3	tone, whole tone, whole step
2	major second	M2	tone, whole tone, whole step		sesquioctavum (9:8)
3	minor third	m3			semiditone (32:27)	sesquiquintum (6:5)
4	major third	M3			ditone (81:64)	sesquiquartum (5:4)
5	perfect fourth	P4	diatessaron		sesquitertium (4:3)
6	diminished fifth	d5	tritone (TT)
6	augmented fourth	A4	tritone (TT)
7	perfect fifth	P5	diapente		sesquialterum (3:2)
12	(perfect) octave	P8	diapason		duplex (2:1)

Additionally, some cultures around the world have their own names for intervals found in their music. For instance, 22 kinds of intervals, called shrutis, are canonically defined in Indian classical music.

Pitch-class intervals

Post-tonal or atonal theory, originally developed for equal tempered European classical music written using the twelve tone technique or serialism, integer notation is often used, most prominently in musical set theory. In this system intervals are named according to the number of half steps, from 0 to 11, the largest interval class being 6.

In atonal or musical set theory there are numerous types of intervals, the first being ordered pitch interval, the distance between two pitches upward or downward. For instance, the interval from C to G upward is 7, but the interval from G to C downward is −7. One can also measure the distance between two pitches without taking into account direction with the unordered pitch interval, somewhat similar to the interval of tonal theory.

The interval between pitch classes may be measured with ordered and unordered pitch-class intervals. The ordered one, also called directed interval, may be considered the measure upwards, which, since we are dealing with pitch classes, depends on whichever pitch is chosen as 0. For unordered pitch-class intervals, see interval class.^[11]

Generic and specific intervals

In diatonic set theory, specific and generic intervals are distinguished. Specific intervals are the interval class or number of semitones between scale steps or collection members, and generic intervals are the number of diatonic scale steps (or staff positions) between notes of a collection or scale.

Notice that staff positions, when used to determine the conventional interval number (second, third, fourth, etc.), are counted including the position of the lower note of the interval, while generic interval numbers are counted excluding that position. Thus, generic interval numbers are smaller by 1, with respect to the conventional interval numbers.

Comparison

Specific interval		Generic interval	Diatonic name
Number of semitones	Interval class	Generic interval	Diatonic name
0	0	0	Perfect unison
1	1	1	Minor second
2	2	1	Major second
3	3	2	Minor third
4	4	2	Major third
5	5	3	Perfect fourth
6	6	3 4	Augmented fourth Diminished fifth
7	5	4	Perfect fifth
8	4	5	Minor sixth
9	3	5	Major sixth
10	2	6	Minor seventh
11	1	6	Major seventh
12	0	7	Perfect octave

Generalizations and non-pitch uses

The term "interval" can also be generalized to other music elements besides pitch. David Lewin's Generalized Musical Intervals and Transformations uses interval as a generic measure of distance to show musical transformations that can change—for instance—one rhythm into another, or one formal structure into another.^[12]^[13]

Notes

↑ ^1.0 ^1.1 Károlyi, Otto (1965), Introducing Music, p. 63. Hammondsworth (England), and New York: Penguin Books. ISBN 0140206590.
↑ Lindley, Mark/Campbell, Murray/Greated, Clive. "Interval", Grove Music Online, ed. L. Macy (accessed 27 February 2007), grovemusic.com (subscription access).
↑ Lindley, Mark/Campbell, Murray/Greated, Clive . " Interval ", Grove Music Online, ed. L. Macy (accessed 27 February 2007), grovemusic.com (subscription access).
↑ ^4.0 ^4.1 ^4.2 Cope, David (1997). Techniques of the Contemporary Composer, pp. 40–41. New York, New York: Schirmer Books. ISBN 0-02-864737-8.
↑ Wyatt, Keith (1998). Harmony & Theory…. Hal Leonard Corporation. pp. 77. ISBN 0793579910.
↑ Aikin, Jim (2004). A Player's Guide to Chords and Harmony: Music Theory for Real-World Musicians, p. 24. ISBN 0-87930-798-6.
↑ Kostka, Stephen; Payne, Dorothy (2008). Tonal Harmony, p. 21. First Edition, 1984.
↑ Prout, Ebenezer (1903). Harmony: Its Theory and Practice, 16th edition. London: Augener & Co. (facsimile reprint, St. Clair Shores, Mich.: Scholarly Press, 1970), p. 10. ISBN 0-403-00326-1.
↑ Hindemith, Paul (1934). The Craft of Musical Composition. New York: Associated Music Publishers. Cited in Cope (1997), p. 40-41.
↑ Perle, George (1990). The Listening Composer, p. 21. California: University of California Press. ISBN 0-520-06991-9.
↑ Roeder, John. "Interval Class", Grove Music Online, ed. L. Macy (accessed 27 February 2007), grovemusic.com (subscription access).
↑ Lewin, David (1987). Generalized Musical Intervals and Transformations, for example sections 3.3.1 and 5.4.2. New Haven: Yale University Press. Reprinted Oxford University Press, 2007. ISBN 978-0-19-531713-8
↑ Ockelford, Adam (2005). Repetition in Music: Theoretical and Metatheoretical Perspectives, p. 7. ISBN 0-7546-3573-2.

External links

Intervals (list)

Numbers in brackets are the number of semitones in the interval.
Fractional semitones are approximate.

Twelve-semitone
(Western)

Perfect	unison (0) · fourth (5) · fifth (7) · octave (12) · fifteenth (24)

Major	second (2) · third (4) · sixth (9) · seventh (11)

Minor	second (1) · third (3) · sixth (8) · seventh (10)

Augmented	unison (1) · second (3) · third (5) · fourth (6) · fifth (8) · sixth (10) · seventh (12) · octave (13)

Diminished	unison (-1) · second (0) · third (2) · fourth (4) · fifth (6) · sixth (7) · seventh (9) · octave (11)

Compound	ninth (13 or 14) · tenth (15 or 16) · eleventh (17) · thirteenth (18 or 19)

Other systems

Supermajor	second (2½) · third (4½) · sixth (9½) · seventh (11½)

Neutral	second (1½) · third (3½) · sixth (8½) · seventh (10½)

Subminor	second (½) · third (2½) · sixth (7½) · seventh (9½)

Other intervals

Groups	Microtone · Comma · Pseudo-octave · Pythagorean interval

Commas	Pythagorean comma · Pythagorean apotome · Pythagorean limma · Diesis · Septimal diesis · Septimal comma · Syntonic comma · Schisma · Diaschisma · Major limma · Ragisma · Breedsma · Kleisma · Septimal kleisma · Septimal semicomma · Orwell comma · Semicomma · Septimal sixth-tone · Septimal quarter tone · Septimal third-tone · Septimal chromatic semitone

Measurement	Cent · Millioctave · Savart

Others	Quarter tone · Wolf · Ditone · Semiditone · Holdrian comma · Secor

Consonance and dissonance

Consonance and dissonance · Preparation · Resolution · Cadence Note · Interval · Chord Nonchord tone · Pedal point · Cambiata

List of musical intervals